Xrthnty

本条目需要擴充。（2013年4月26日） 请協助改善这篇條目，更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。

加性高斯白噪声（英语：Additive white Gaussian noise，AWGN）在通信领域中指的是一种功率谱函数是常数（即白噪声），且幅度服从高斯分布的噪声信号。因其可加性、幅度服从高斯分布且为白噪声的一种而得名。

该噪声信号为一种便于分析的理想噪声信号，实际的噪声信号往往只在某一频段内可以用高斯白噪声的特性来进行近似处理。由于AWGN信号易于分析、近似，因此在信号处理领域，对信号处理系统（如滤波器、低噪音高频放大器、无线信号传输等）的噪声性能的简单分析(如：信噪比分析)中，一般可假设系统所产生的噪音或受到的噪音信号干扰在某频段或限制条件之下是高斯白噪声。

加性高斯白噪声只是白噪声的一种，另有泊松白噪声等。

信道容量

AWGN 信道由一系列的Yidisplaystyle Y_i（输出） 来表示，其中的 idisplaystyle i 表示离散的时间事件索引。Yidisplaystyle Y_i 是 Xidisplaystyle X_i（输入）、噪声、Zidisplaystyle Z_i 的数值和，其中 Zidisplaystyle Z_i 是独立恒等分布的随机变量并来自于均值为 0，方差为 Ndisplaystyle N（噪声） 的正态分布。Zidisplaystyle Z_i 可以进一步认为和 Xidisplaystyle X_i 有关。

Zi∼N(0,N)displaystyle Z_isim mathcal N(0,N),!

Yi=Xi+Zi∼N(Xi,N).displaystyle Y_i=X_i+Z_isim mathcal N(X_i,N).,!

信道的容量是无穷的，除非噪声 ndisplaystyle n 非零且 Xidisplaystyle X_i 有足够的约束。输入中最常见的约束被叫做功率约束，这要求码字(x1,x2,…,xk)displaystyle (x_1,x_2,dots ,x_k) 通过信道传送。我们有：

1k∑i=1kxi2≤P,displaystyle frac 1ksum _i=1^kx_i^2leq P,,!

其中 Pdisplaystyle P 代表信道功率的最大值。因此信道容量的功率约束可以通过以下公式给出：

C=maxf(x) s.t. E(X2)≤PI(X;Y)displaystyle C=max _f(x)text s.t. Eleft(X^2right)leq PI(X;Y),!

这里，f(x)displaystyle f(x) 是 Xdisplaystyle X 的分布。I(X;Y)displaystyle I(X;Y) 可以扩展为微分熵的形式：

I(X;Y)=h(Y)−h(Y|X)=h(Y)−h(X+Z|X)=h(Y)−h(Z|X)displaystyle X)&=h(Y)-h(Z,!

但是 Xdisplaystyle X 和 Zdisplaystyle Z 是独立的，因此：

I(X;Y)=h(Y)−h(Z)displaystyle I(X;Y)=h(Y)-h(Z),!

通过计算高斯微分熵可给出：

h(Z)=12log⁡(2πeN)displaystyle h(Z)=frac 12log(2pi eN),!

因为 Xdisplaystyle X 和 Zdisplaystyle Z 是独立的并且它们的和给出了 Ydisplaystyle Y：

E(Y2)=E(X+Z)2=E(X2)+2E(X)E(Z)+E(Z2)=P+Ndisplaystyle E(Y^2)=E(X+Z)^2=E(X^2)+2E(X)E(Z)+E(Z^2)=P+N,!

从此约束中，我们可以从微分熵的属性中推断出：

h(Y)≤12log⁡(2πe(P+N))displaystyle h(Y)leq frac 12log(2pi e(P+N)),!

因此通道容量可以通过可变信息中的最高可获取约束求得：

I(X;Y)≤12log⁡(2πe(P+N))−12log⁡(2πeN)displaystyle I(X;Y)leq frac 12log(2pi e(P+N))-frac 12log(2pi eN),!

其中 I(X;Y)displaystyle I(X;Y) 在

X∼N(0,P)displaystyle Xsim mathcal N(0,P),!

时最大。

因此 AWGN 的信道容量 Cdisplaystyle C可以由此给出：

C=12log⁡(1+PN)displaystyle C=frac 12log left(1+frac PNright),!

时间域中的效果

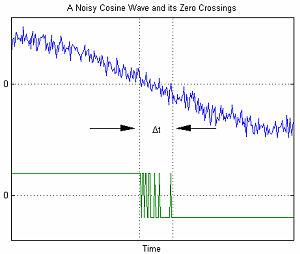
Zero-Crossings of a Noisy Cosine

在串行数据通信中，AWGN 数学模型被用来对由随机抖动引发的时间性错误建模。

右图中展示了和 AWGN 关联的时间性错误。变量 Δtdisplaystyle Delta t 表示零点交叉处的不确定性。当 AWGN 中的振幅被提升时，信噪比降低。这导致不确定性 Δtdisplaystyle Delta t 降低。

当受 AWGN 影响时。当输入是一个正弦波时，窄通频带滤波输出中的每一秒，不管是正向趋近于零点交叉还是负趋向于零点交叉的平均数都是：

positive zero crossingssecond=negative zero crossingsseconddisplaystyle frac mathrm positive zero crossings mathrm second =frac mathrm negative zero crossings mathrm second

=f0SNR+1+B212f02SNR+1displaystyle =f_0sqrt frac mathrm SNR +1+frac B^212f_0^2mathrm SNR +1

其中

• f₀ = 滤波的中心频率


• B = 滤波器带宽


• SNR = 线性关系上的信噪功率比

參照

• 接地反弹


• 有噪信道编码定理


• 高斯过程