Xrthnty

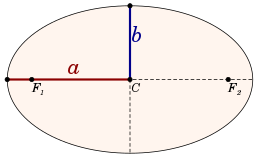
The semi-major (a) and semi-minor axis (b) of an ellipse

In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the widest points of the perimeter. The semi-major axis is one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. For the special case of a circle, the semi-major axis is the radius.

The length of the semi-major axis adisplaystyle a of an ellipse is related to the semi-minor axis's length bdisplaystyle b through the eccentricity edisplaystyle e and the semi-latus rectum ℓdisplaystyle ell , as follows:

b=a1−e2,ℓ=a(1−e2),aℓ=b2.displaystyle beginalignedb&=asqrt 1-e^2,,\ell &=aleft(1-e^2right),,\aell &=b^2.,endaligned

The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the center to either vertex of the hyperbola.

A parabola can be obtained as the limit of a sequence of ellipses where one focus is kept fixed as the other is allowed to move arbitrarily far away in one direction, keeping ℓdisplaystyle ell fixed. Thus adisplaystyle a and bdisplaystyle b tend to infinity, adisplaystyle a faster than bdisplaystyle b.

The semi-minor axis of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section.

The major and minor axes are the axes of symmetry for the curve: in an ellipse, the minor axis is the shorter one; in a hyperbola, it is the one that does not intersect the hyperbola.

Ellipse

The equation of an ellipse is:

(x−h)2a2+(y−k)2b2=1.displaystyle frac left(x-hright)^2a^2+frac left(y-kright)^2b^2=1.

Where (h,k) is the center of the ellipse in Cartesian coordinates, in which an arbitrary point is given by (x,y).

The semi-major axis is the mean value of the maximum and minimum distances rmaxdisplaystyle r_max and rmindisplaystyle r_min of the ellipse from a focus — that is, of the distances from a focus to the endpoints of the major axis. In astronomy these extreme points are called apsides.

a=rmax+rmin2.displaystyle a=frac r_max +r_min 2.

The semi-minor axis of an ellipse is the geometric mean of these distances:

b=rmaxrmin.displaystyle b=sqrt r_max r_min .

The eccentricity of an ellipse is defined as

e=1−b2a2displaystyle e=sqrt 1-frac b^2a^2 so rmin=a(1−e),rmax=a(1+e)displaystyle r_min =a(1-e),r_max =a(1+e).

Now consider the equation in polar coordinates, with one focus at the origin and the other on the (θ=π)−displaystyle (theta =pi )-direction,

r(1+ecos⁡θ)=ℓ.displaystyle r(1+ecos theta )=ell .,

The mean value of r=ℓ/(1−e)displaystyle r=ell /(1-e) and r=ℓ/(1+e)displaystyle r=ell /(1+e), for θ=πdisplaystyle theta =pi and θ=0displaystyle theta =0 is

a=ℓ1−e2.displaystyle a=ell over 1-e^2.,

In an ellipse, the semi-major axis is the geometric mean of the distance from the center to either focus and the distance from the center to either directrix.

The semi-minor axis of an ellipse runs from the center of the ellipse (a point halfway between and on the line running between the foci) to the edge of the ellipse. The semi-minor axis is half of the minor axis. The minor axis is the longest line segment perpendicular to the major axis that connects two points on the ellipse's edge.

The semi-minor axis bdisplaystyle b is related to the semi-major axis adisplaystyle a through the eccentricity edisplaystyle e and the semi-latus rectum ℓdisplaystyle ell , as follows:

b=a1−e2aℓ=b2.displaystyle beginalignedb&=asqrt 1-e^2,!\aell &=b^2.,!endaligned

A parabola can be obtained as the limit of a sequence of ellipses where one focus is kept fixed as the other is allowed to move arbitrarily far away in one direction, keeping ℓdisplaystyle ell fixed. Thus adisplaystyle a and bdisplaystyle b tend to infinity, adisplaystyle a faster than bdisplaystyle b.

The length of the semi-minor axis could also be found using the following formula,^[1]

2b=(p+q)2−f2displaystyle 2b=sqrt (p+q)^2-f^2

where fdisplaystyle f is the distance between the foci, pdisplaystyle p and qdisplaystyle q are the distances from each focus to any point in the ellipse.

Hyperbola

The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches; if this is adisplaystyle a in the x-direction the equation is:

(x−h)2a2−(y−k)2b2=1.displaystyle frac left(x-hright)^2a^2-frac left(y-kright)^2b^2=1.

In terms of the semi-latus rectum and the eccentricity we have

a=ℓ1−e2.displaystyle a=ell over 1-e^2.

The transverse axis of a hyperbola coincides with the major axis.^[2]

In a hyperbola, a conjugate axis or minor axis of length 2bdisplaystyle 2b, corresponding to the minor axis of an ellipse, can be drawn perpendicular to the transverse axis or major axis, the latter connecting the two vertices (turning points) of the hyperbola, with the two axes intersecting at the center of the hyperbola. The endpoints (0,±b)displaystyle (0,pm b) of the minor axis lie at the height of the asymptotes over/under the hyperbola's vertices. Either half of the minor axis is called the semi-minor axis, of length bdisplaystyle b. Denoting the semi-major axis length (distance from the center to a vertex) as adisplaystyle a, the semi-minor and semi-major axes' lengths appear in the equation of the hyperbola relative to these axes as follows:

x2a2−y2b2=1.displaystyle frac x^2a^2-frac y^2b^2=1.

The semi-minor axis is also the distance from one of focuses of the hyperbola to an asymptote. Often called the impact parameter, this is important in physics and astronomy, and measure the distance a particle will miss the focus by if its journey is unperturbed by the body at the focus.

The semi-minor axis and the semi-major axis are related through the eccentricity, as follows:

b=ae2−1.displaystyle b=asqrt e^2-1.^[3]

Note that in a hyperbola bdisplaystyle b can be larger than adisplaystyle a.
[1]

Astronomy

Orbital period

In astrodynamics the orbital period Tdisplaystyle T of a small body orbiting a central body in a circular or elliptical orbit is:

T=2πa3μdisplaystyle T=2pi sqrt a^3 over mu

where:

adisplaystyle a is the length of the orbit's semi-major axis

μdisplaystyle mu is the standard gravitational parameter of the central body

Note that for all ellipses with a given semi-major axis, the orbital period is the same, disregarding their eccentricity.

The specific angular momentum Hdisplaystyle H of a small body orbiting a central body in a circular or elliptical orbit is:

H=aμ(1−e2)displaystyle H=sqrt amu left(1-e^2right)

where:

adisplaystyle a and μdisplaystyle mu are as defined above

edisplaystyle e is the eccentricity of the orbit

In astronomy, the semi-major axis is one of the most important orbital elements of an orbit, along with its orbital period. For Solar System objects, the semi-major axis is related to the period of the orbit by Kepler's third law (originally empirically derived),

T2∝a3displaystyle T^2propto a^3,

where Tdisplaystyle T is the period and adisplaystyle a is the semi-major axis. This form turns out to be a simplification of the general form for the two-body problem, as determined by Newton:

T2=4π2G(M+m)a3displaystyle T^2=frac 4pi ^2G(M+m)a^3,

where Gdisplaystyle G is the gravitational constant, Mdisplaystyle M is the mass of the central body, and mdisplaystyle m is the mass of the orbiting body. Typically, the central body's mass is so much greater than the orbiting body's, that mdisplaystyle m may be ignored. Making that assumption and using typical astronomy units results in the simpler form Kepler discovered.

The orbiting body's path around the barycentre and its path relative to its primary are both ellipses. The semi-major axis is sometimes used in astronomy as the primary-to-secondary distance when the mass ratio of the primary to the secondary is significantly large (M≫mdisplaystyle Mgg m); thus, the orbital parameters of the planets are given in heliocentric terms. The difference between the primocentric and "absolute" orbits may best be illustrated by looking at the Earth–Moon system. The mass ratio in this case is 7001813005900000000♠81.30059. The Earth–Moon characteristic distance, the semi-major axis of the geocentric lunar orbit, is 384,400 km. The barycentric lunar orbit, on the other hand, has a semi-major axis of 379,700 km, the Earth's counter-orbit taking up the difference, 4,700 km. The Moon's average barycentric orbital speed is 1.010 km/s, whilst the Earth's is 0.012 km/s. The total of these speeds gives a geocentric lunar average orbital speed of 1.022 km/s; the same value may be obtained by considering just the geocentric semi-major axis value.

Average distance

It is often said that the semi-major axis is the "average" distance between the primary focus of the ellipse and the orbiting body. This is not quite accurate, because it depends on what the average is taken over.

• averaging the distance over the eccentric anomaly indeed results in the semi-major axis.


• averaging over the true anomaly (the true orbital angle, measured at the focus) results, oddly enough, in the semi-minor axis b=a1−e2displaystyle b=asqrt 1-e^2.


• averaging over the mean anomaly (the fraction of the orbital period that has elapsed since pericentre, expressed as an angle), finally, gives the time-average a(1+e22).displaystyle aleft(1+frac e^22right).,
  

The time-averaged value of the reciprocal of the radius, r−1displaystyle r^-1, is a−1displaystyle a^-1.

Energy; calculation of semi-major axis from state vectors

In astrodynamics, the semi-major axis adisplaystyle a can be calculated from orbital state vectors:

a=−μ2εdisplaystyle a=-mu over 2varepsilon ,

for an elliptical orbit and, depending on the convention, the same or

a=μ2εdisplaystyle a=mu over 2varepsilon ,

for a hyperbolic trajectory

and

ε=v22−μ|r|displaystyle varepsilon =v^2 over 2-mathbf r right

(specific orbital energy)

and

μ=GMdisplaystyle mu =GM,

(standard gravitational parameter), where:

• 
  vdisplaystyle v is orbital velocity from velocity vector of an orbiting object,


• 
  r is a cartesian position vector of an orbiting object in coordinates of a reference frame with respect to which the elements of the orbit are to be calculated (e.g. geocentric equatorial for an orbit around Earth, or heliocentric ecliptic for an orbit around the Sun),


• 
  Gdisplaystyle G is the gravitational constant,


• 
  Mdisplaystyle M is the mass of the gravitating body, and


• 
  εdisplaystyle varepsilon is the specific energy of the orbiting body.

Note that for a given amount of total mass, the specific energy and the semi-major axis are always the same, regardless of eccentricity or the ratio of the masses. Conversely, for a given total mass and semi-major axis, the total specific orbital energy is always the same. This statement will always be true under any given conditions.

See also

• Semidiameter

References

External links

• 
  Semi-major and semi-minor axes of an ellipse With interactive animation