Xrthnty

Absolute magnitude is a measure of the luminosity of a celestial object, on a logarithmic astronomical magnitude scale. An object's absolute magnitude is defined to be equal to the apparent magnitude that the object would have if it were viewed from a distance of exactly 10 parsecs (32.6 light-years), with no extinction (or dimming) of its light due to absorption by interstellar dust particles. By hypothetically placing all objects at a standard reference distance from the observer, their luminosities can be directly compared on a magnitude scale. As with all astronomical magnitudes, the absolute magnitude can be specified for different wavelength ranges corresponding to specified filter bands or passbands; for stars a commonly quoted absolute magnitude is the absolute visual magnitude, which uses the visual (V) band of the spectrum (in the UBV photometric system). Absolute magnitudes are denoted by a capital M, with a subscript representing the filter band used for measurement, such as M_V for absolute magnitude in the V band.

The more luminous an object, the smaller the numerical value of its absolute magnitude. A difference of 5 magnitudes between the absolute magnitudes of two objects corresponds to a ratio of 100 in their luminosities, and a difference of n magnitudes in absolute magnitude corresponds to a luminosity ratio of 100^(n/5). For example, a star of absolute magnitude M_V=3 would be 100 times more luminous than a star of absolute magnitude M_V=8 as measured in the V filter band. The Sun has absolute magnitude M_V=+4.83.^[1] Highly luminous objects can have negative absolute magnitudes: for example, the Milky Way galaxy has an absolute B magnitude of about −20.8.^[2]

An object's absolute bolometric magnitude represents its total luminosity over all wavelengths, rather than in a single filter band, as expressed on a logarithmic magnitude scale. To convert from an absolute magnitude in a specific filter band to absolute bolometric magnitude, a bolometric correction is applied.

For Solar System bodies that shine in reflected light, a different definition of absolute magnitude (H) is used, based on a standard reference distance of one astronomical unit.

Stars and galaxies (M)

In stellar and galactic astronomy, the standard distance is 10 parsecs (about 32.616 light-years, 308.57 petameters or 308.57 trillion kilometres). A star at 10 parsecs has a parallax of 0.1″ (100 milliarcseconds). Galaxies (and other extended objects) are much larger than 10 parsecs, their light is radiated over an extended patch of sky, and their overall brightness cannot be directly observed from relatively short distances, but the same convention is used. A galaxy's magnitude is defined by measuring all the light radiated over the entire object, treating that integrated brightness as the brightness of a single point-like or star-like source, and computing the magnitude of that point-like source as it would appear if observed at the standard 10 parsecs distance. Consequently, the absolute magnitude of any object equals the apparent magnitude it would have if it were 10 parsecs away.

The measurement of absolute magnitude is made with an instrument called a bolometer. When using an absolute magnitude, one must specify the type of electromagnetic radiation being measured. When referring to total energy output, the proper term is bolometric magnitude. The bolometric magnitude usually is computed from the visual magnitude plus a bolometric correction, M_bol = M_V + BC. This correction is needed because very hot stars radiate mostly ultraviolet radiation, whereas very cool stars radiate mostly infrared radiation (see Planck's law).

Some stars visible to the naked eye have such a low absolute magnitude that they would appear bright enough to outshine the planets and cast shadows if they were at 10 parsecs from the Earth. Examples include Rigel (−7.0), Deneb (−7.2), Naos (−6.0), and Betelgeuse (−5.6). For comparison, Sirius has an absolute magnitude of 1.4, which is brighter than the Sun, whose absolute visual magnitude is 4.83 (it actually serves as a reference point). The Sun's absolute bolometric magnitude is set arbitrarily, usually at 4.75.^[3][4]
Absolute magnitudes of stars generally range from −10 to +17. The absolute magnitudes of galaxies can be much lower (brighter). For example, the giant elliptical galaxy M87 has an absolute magnitude of −22 (i.e. as bright as about 60,000 stars of magnitude −10).

Apparent magnitude

The Greek astronomer Hipparchus established a numerical scale to describe the brightness of each star appearing in the sky. The brightest stars in the sky were assigned an apparent magnitude m = 1, and the dimmest stars visible to the naked eye are assigned m = 6.^[5] The difference between them corresponds to a factor of 100 in brightness. For objects within the immediate neighborhood of the Sun, the absolute magnitude M and apparent magnitude m from any distance d (in parsecs) is related by:

100m−M5=F10F=(d10pc)2,displaystyle 100^frac m-M5=frac F_10F=left(frac d10;mathrm pc right)^2,

where F is the radiant flux measured at distance d (in parsecs), F₁₀ the radiant flux measured at distance 10 pc. The relation can be written in terms of logarithm:

M=m−5(log10⁡(dpc)−1),displaystyle M=m-5left(log _10(d_textpc)-1right),

where the insignificance of extinction by gas and dust is assumed. Typical extinction rates within the galaxy are 1 to 2 magnitudes per kiloparsec, when dark clouds are taken into account.^[6]

For objects at very large distances (outside the Milky Way) the luminosity distance d_L must be used instead of d (in parsecs), because the Euclidean approximation is invalid for distant objects and general relativity must be taken into account. Moreover, the cosmological redshift complicates the relation between absolute and apparent magnitude, because the radiation observed was shifted into the red range of the spectrum. To compare the magnitudes of very distant objects with those of local objects, a K correction might have to be applied to the magnitudes of the distant objects.

The absolute magnitude M can also be approximated using apparent magnitude m and stellar parallax p:

M=m+5(log10⁡p+1),displaystyle M=m+5left(log _10p+1right),

or using apparent magnitude m and distance modulus μ:

M=m−μdisplaystyle M=m-mu .

Examples

Rigel has a visual magnitude m_V of 0.12 and distance about 860 light-years

MV=0.12−5(log10⁡8603.2616−1)=−7.0.displaystyle M_mathrm V =0.12-5left(log _10frac 8603.2616-1right)=-7.0.

Vega has a parallax p of 0.129″, and an apparent magnitude m_V of 0.03

MV=0.03+5(log10⁡0.129+1)=+0.6.displaystyle M_mathrm V =0.03+5left(log _100.129+1right)=+0.6.

Alpha Centauri A has a parallax p of 0.742″ and an apparent magnitude m_V of −0.01

MV=−0.01+5(log10⁡0.742+1)=+4.3.displaystyle M_mathrm V =-0.01+5left(log _100.742+1right)=+4.3.

The Black Eye Galaxy has a visual magnitude m_V of 9.36 and a distance modulus μ of 31.06

MV=9.36−31.06=−21.7.displaystyle M_mathrm V =9.36-31.06=-21.7.

Bolometric magnitude

The bolometric magnitude M_bol, takes into account electromagnetic radiation at all wavelengths. It includes those unobserved due to instrumental passband, the Earth's atmospheric absorption, and extinction by interstellar dust. It is defined based on the luminosity of the stars. In the case of stars with few observations, it must be computed assuming an effective temperature.

Classically, the difference in bolometric magnitude is related to the luminosity ratio according to:

Mbol,⋆−Mbol,⊙=−2.5log10⁡(L⋆L⊙)displaystyle M_mathrm bol,star -M_mathrm bol,odot =-2.5log _10left(frac L_star L_odot right)

which makes by inversion:

L⋆L⊙=100.4(Mbol,⊙−Mbol,⋆)displaystyle frac L_star L_odot =10^0.4left(M_mathrm bol,odot -M_mathrm bol,star right)

where

L_⊙ is the Sun's luminosity (bolometric luminosity)

L_★ is the star's luminosity (bolometric luminosity)

M_bol,⊙ is the bolometric magnitude of the Sun

M_bol,★ is the bolometric magnitude of the star.

In August 2015, the International Astronomical Union passed Resolution B2^[7] defining the zero points of the absolute and apparent bolometric magnitude scales in SI units for power (watts) and irradiance (W/m²), respectively. Although bolometric magnitudes had been used by astronomers for many decades, there had been systematic differences in the absolute magnitude-luminosity scales presented in various astronomical references, and no international standardization. This led to systematic differences in bolometric corrections scales.^[8] Combined with incorrect assumed absolute bolometric magnitudes for the Sun could lead to systematic errors in estimated stellar luminosities (and stellar properties calculated which rely on stellar luminosity, such as radii, ages, and so on).

Resolution B2 defines an absolute bolometric magnitude scale where M_bol = 0 corresponds to luminosity L₀ = 7028301280000000000♠3.0128×10²⁸ W, with the zero point luminosity L₀ set such that the Sun (with nominal luminosity 7026382800000000000♠3.828×10²⁶ W) corresponds to absolute bolometric magnitude M_bol,⊙ = 4.74. Placing a radiation source (e.g. star) at the standard distance of 10 parsecs, it follows that the zero point of the apparent bolometric magnitude scale m_bol = 0 corresponds to irradiance f₀ = 6992251802100199999♠2.518021002×10⁻⁸ W/m². Using the IAU 2015 scale, the nominal total solar irradiance ("solar constant") measured at 1 astronomical unit (7003136100000000000♠1361 W/m²) corresponds to an apparent bolometric magnitude of the Sun of m_bol,⊙ = −26.832.^[8]

Following Resolution B2, the relation between a star's absolute bolometric magnitude and its luminosity is no longer directly tied to the Sun's (variable) luminosity:

Mbol=−2.5log10⁡L⋆L0≈−2.5log10⁡L⋆+71.197425displaystyle M_mathrm bol =-2.5log _10frac L_star L_0approx -2.5log _10L_star +71.197425

where

L_★ is the star's luminosity (bolometric luminosity) in watts

L₀ is the zero point luminosity 7028301280000000000♠3.0128×10²⁸ W

M_bol is the bolometric magnitude of the star

The new IAU absolute magnitude scale permanently disconnects the scale from the variable Sun. However, on this SI power scale, the nominal solar luminosity corresponds closely to M_bol = 4.74, a value that was commonly adopted by astronomers before the 2015 IAU resolution.^[8]

The luminosity of the star in watts can be calculated as a function of its absolute bolometric magnitude M_bol as:

L⋆=L010−0.4Mboldisplaystyle L_star =L_010^-0.4M_mathrm bol

using the variables as defined previously.

Solar System bodies (H)

For planets and asteroids a definition of absolute magnitude that is more meaningful for non-stellar objects is used. The absolute magnitude, commonly called Hdisplaystyle H, is defined as the apparent magnitude that the object would have if it were one Astronomical Unit (AU) from both the Sun and the observer, and in conditions of ideal solar opposition (an arrangement that is impossible in practice).^[9] Solar System bodies are illuminated by the Sun, therefore the magnitude varies as a function of illumination conditions, described by the phase angle. This relationship is referred to as the phase curve. The absolute magnitude is the brightness at phase angle zero, an arrangement known as opposition.

Stellar absolute magnitude, as described in the previous sections, and planetary absolute magnitude differ only by a constant. To convert a stellar absolute magnitude into a planetary one, subtract 31.57displaystyle 31.57.^[10]

Examples: The Sun has an absolute magnitude of MV=+4.83,displaystyle M_V=+4.83, corresponding to H=−26.74displaystyle H=-26.74 (equal to the Sun's apparent magnitude from Earth).^[1] The faintest types of stellar objects, red dwarfs, have absolute magnitudes up to about MV=+20.displaystyle M_V=+20. On the scale for Solar System objects, this corresponds to an absolute magnitude H=−11.57.displaystyle H=-11.57.^[11] The largest planet in the Solar System, Jupiter, has an absolute magnitude of H=−9.4displaystyle H=-9.4,^[12] which on the stellar magnitude scale would be MV=+22.17displaystyle M_V=+22.17.

Apparent magnitude

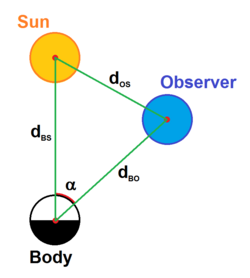
The phase angle αdisplaystyle alpha can be calculated from the distances body-sun, observer-sun and observer-body, using the law of cosines.

The absolute magnitude Hdisplaystyle H can be used to calculate the apparent magnitude mdisplaystyle m of a body. For an object reflecting sunlight, Hdisplaystyle H and mdisplaystyle m are connected by the relation

m=H+5log10⁡(dBSdBOd02)−2.5log10⁡q(α),displaystyle m=H+5log _10left(frac d_BSd_BOd_0^2right)-2.5log _10q(alpha ),

where αdisplaystyle alpha is the phase angle, the angle between the body-Sun and body–observer lines. q(α)displaystyle q(alpha ) is the phase integral (the integration of reflected light; a number in the 0 to 1 range).^[13]

By the law of cosines, we have:

cos⁡α=dBO2+dBS2−dOS22dBOdBS.displaystyle cos alpha =frac d_mathrm BO ^2+d_mathrm BS ^2-d_mathrm OS ^22d_mathrm BO d_mathrm BS .

Distances:

• 
  d_BO is the distance between the body and the observer


• 
  d_BS is the distance between the body and the Sun


• 
  d_OS is the distance between the observer and the Sun


• 
  d₀ is 1 AU, the average distance between the Earth and the Sun

Approximations for phase integral q(α)displaystyle q(alpha )

The value of q(α)displaystyle q(alpha ) depends on the properties of the reflecting surface, in particular on its roughness. In practice, different approximations are used based on the known or assumed properties of the surface.^[13]

Planets

Diffuse reflection on sphere and flat disk

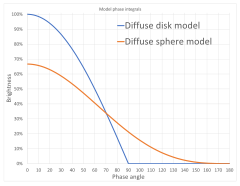
Brightness with phase for diffuse reflection models. The sphere is 2/3 as bright at zero phase, while the disk can't be seen beyond 90 degrees.

Planetary bodies can be approximated reasonably well as ideal diffuse reflecting spheres. Let αdisplaystyle alpha be the phase angle in degrees, then^[14]

q(α)=23((1−α180∘)cos⁡α+1πsin⁡α).displaystyle q(alpha )=frac 23left(left(1-frac alpha 180^circ right)cos alpha +frac 1pi sin alpha right).

A full-phase diffuse sphere reflects two-thirds as much light as a diffuse flat disk of the same diameter. A quarter phase (α=90∘displaystyle alpha =90^circ ) has 1πdisplaystyle frac 1pi as much light as full phase (α=0∘displaystyle alpha =0^circ ).

For contrast, a diffuse disk reflector model is simply q(α)=cos⁡αdisplaystyle q(alpha )=cos alpha , which isn't realistic, but it does represent the opposition surge for rough surfaces that reflect more uniform light back at low phase angles.

The definition of the geometric albedo pdisplaystyle p, a measure for the reflectivity of planetary surfaces, is based on the diffuse disk reflector model. The absolute magnitude Hdisplaystyle H, diameter Ddisplaystyle D (in kilometers) and geometric albedo pdisplaystyle p of a body are related by^[15][16]

D=1329p×10−0.2Hdisplaystyle D=frac 1329sqrt ptimes 10^-0.2H km.

Example: The Moon's absolute magnitude Hdisplaystyle H can be calculated from its diameter D=3474 kmdisplaystyle D=3474text km and geometric albedo p=0.113displaystyle p=0.113:^[17]

H=5log10⁡132934740.113=+0.28.displaystyle H=5log _10frac 13293474sqrt 0.113=+0.28.

We have dBS=1 AUdisplaystyle d_BS=1text AU, dBO=384400 km=0.00257 AU.displaystyle d_BO=384400text km=0.00257text AU.
At quarter phase, q(α)≈23πdisplaystyle q(alpha )approx frac 23pi (according to the diffuse reflector model), this yields an apparent magnitude of m=+0.28+5log10⁡(1⋅0.00257)−2.5log10⁡(23π)=−10.99.displaystyle m=+0.28+5log _10left(1cdot 0.00257right)-2.5log _10left(frac 23pi right)=-10.99. The actual value is somewhat lower than that, m=−10.0.displaystyle m=-10.0. The phase curve of the Moon is too complicated for the diffuse reflector model.^[18]

More advanced models

Because Solar System bodies are never perfect diffuse reflectors, astronomers use different models to predict apparent magnitudes based on known or assumed properties of the body.^[13] For planets, approximations for the correction term −2.5log10⁡q(α)displaystyle -2.5log _10q(alpha ) in the formula for m have been derived empirically, to match observations at different phase angles. The approximations recommended by the Astronomical Almanac^[12] are (with αdisplaystyle alpha in degrees):

Planet	Hdisplaystyle H	Approximation for −2.5log10⁡q(α)displaystyle -2.5log _10q(alpha )
Mercury	−0.613	+6.328×10−2α−1.6336×10−3α2+3.3644×10−5α3−3.4265×10−7α4+1.6893×10−9α5−3.0334×10−12α6displaystyle +6.328times 10^-2alpha -1.6336times 10^-3alpha ^2+3.3644times 10^-5alpha ^3-3.4265times 10^-7alpha ^4+1.6893times 10^-9alpha ^5-3.0334times 10^-12alpha ^6
Venus	−4.384	−1.044×10−3α+3.687×10−4α2−2.814×10−6α3+8.938×10−9α4displaystyle -1.044times 10^-3alpha +3.687times 10^-4alpha ^2-2.814times 10^-6alpha ^3+8.938times 10^-9alpha ^4 (for 0∘<α≤163.7∘displaystyle 0^circ <alpha leq 163.7^circ ) +240.44228−2.81914α+8.39034×10−3α2displaystyle +240.44228-2.81914alpha +8.39034times 10^-3alpha ^2 (for 163.7∘<α<179∘displaystyle 163.7^circ <alpha <179^circ )
Earth	−3.99a	−1.060×10−3α+2.054×10−4α2displaystyle -1.060times 10^-3alpha +2.054times 10^-4alpha ^2
Mars	−1.601	+2.267×10−2α−1.302×10−4α2displaystyle +2.267times 10^-2alpha -1.302times 10^-4alpha ^2 (for 0∘<α≤50∘displaystyle 0^circ <alpha leq 50^circ ) +1.234−2.573×10−2α+3.445×10−4α2displaystyle +1.234-2.573times 10^-2alpha +3.445times 10^-4alpha ^2 (for 50∘<α≤120∘displaystyle 50^circ <alpha leq 120^circ )
Jupiter	−9.395	−3.7×10−4α+6.16×10−4α2displaystyle -3.7times 10^-4alpha +6.16times 10^-4alpha ^2 (for α≤12∘displaystyle alpha leq 12^circ ) −0.033−2.5log10⁡(1−1.507(α180∘)−0.363(α180∘)2−0.062(α180∘)3+2.809(α180∘)4−1.876(α180∘)5)displaystyle -0.033-2.5log _10left(1-1.507left(frac alpha 180^circ right)-0.363left(frac alpha 180^circ right)^2-0.062left(frac alpha 180^circ right)^3+2.809left(frac alpha 180^circ right)^4-1.876left(frac alpha 180^circ right)^5right) (for α>12∘displaystyle alpha >12^circ )
Saturn	−8.914	1.825sin⁡(β)+2.6×10−2α−0.378sin⁡(β)e−2.25αdisplaystyle 1.825sin left(beta right)+2.6times 10^-2alpha -0.378sin left(beta right)e^-2.25alpha (for planet and rings, α<6.5∘displaystyle alpha <6.5^circ and β<27∘displaystyle beta <27^circ ) −0.036−3.7×10−4α+6.16×10−4α2displaystyle -0.036-3.7times 10^-4alpha +6.16times 10^-4alpha ^2 (for the globe alone, α≤6∘displaystyle alpha leq 6^circ ) +0.026+2.446×10−4α+2.672×10−4α2−1.505×10−6α3+4.767×10−9α4displaystyle +0.026+2.446times 10^-4alpha +2.672times 10^-4alpha ^2-1.505times 10^-6alpha ^3+4.767times 10^-9alpha ^4 (for the globe alone, 6∘<α<150∘displaystyle 6^circ <alpha <150^circ )
Uranus	−7.110	−8.4×10−4ϕ′+6.587×10−3α+1.045×10−4α2displaystyle -8.4times 10^-4phi '+6.587times 10^-3alpha +1.045times 10^-4alpha ^2 (for α<3.1∘displaystyle alpha <3.1^circ )
Neptune	−7.00	+7.944×10−3α+9.617×10−5α2displaystyle +7.944times 10^-3alpha +9.617times 10^-5alpha ^2 (for α<133∘displaystyle alpha <133^circ and t>2000.0displaystyle t>2000.0)

Here βdisplaystyle beta is the effective inclination of Saturn's rings (their tilt relative to the observer), which as seen from Earth varies between 0° and 27° over the course of one Saturn orbit, and ϕ′displaystyle phi ' is a small correction term depending on Uranus' sub-Earth and sub-solar latitudes. tdisplaystyle t is the Common Era year. Neptune's absolute magnitude is changing slowly due to seasonal effects as the planet moves along its 165-year orbit around the Sun, and the approximation above is only valid after the year 2000. For some circumstances, like α≥179∘displaystyle alpha geq 179^circ for Venus, no observations are available, and the phase curve is unknown in those cases.

Example: On 1 January 2019, Venus was dBS=0.719 AUdisplaystyle d_BS=0.719text AU from the Sun, and dBO=0.645 AUdisplaystyle d_BO=0.645text AU from Earth, at a phase angle of α=93.0∘displaystyle alpha =93.0^circ (near quarter phase). Under full-phase conditions, Venus would have been visible at m=−4.384+5log10⁡(0.719⋅0.645)=−6.09.displaystyle m=-4.384+5log _10left(0.719cdot 0.645right)=-6.09. Accounting for the high phase angle, the correction term above yields an actual apparent magnitude of m=−6.09+(−1.044×10−3⋅93.0+3.687×10−4⋅93.02−2.814×10−6⋅93.03+8.938×10−9⋅93.04)=−4.59.displaystyle m=-6.09+left(-1.044times 10^-3cdot 93.0+3.687times 10^-4cdot 93.0^2-2.814times 10^-6cdot 93.0^3+8.938times 10^-9cdot 93.0^4right)=-4.59. This is close to the value of m=−4.62displaystyle m=-4.62 predicted by the Jet Propulsion Laboratory.^[19]

• 
  ^aEarth's albedo varies by a factor of 6, from 0.12 in the cloud-free case to 0.76 in the case of altostratus cloud. The absolute magnitude here corresponds to an albedo of 0.434. Earth's apparent magnitude cannot be predicted as accurately as that of most other planets.^[12]

Asteroids

Asteroid 1 Ceres, imaged by the Dawn spacecraft at phase angles of 0°, 7° and 33°. The left image at 0° phase angle shows the brightness surge due to the opposition effect.

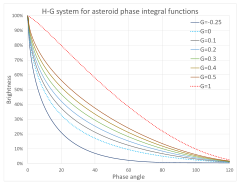
Phase integrals for various values of G

Relation between the slope parameter Gdisplaystyle G and the opposition surge. Larger values of Gdisplaystyle G correspond to a less pronounced opposition effect. For most asteroids, a value of G=0.15displaystyle G=0.15 is assumed, corresponding to an opposition surge of 0.3 magdisplaystyle 0.3text mag.

If an object has an atmosphere, it reflects light more or less isotropically in all directions, and its brightness can be modelled as a diffuse reflector. Atmosphereless bodies, like asteroids or moons, tend to reflect light more strongly to the direction of the incident light, and their brightness increases rapidly as the phase angle approaches 0∘displaystyle 0^circ . This rapid brightening near opposition is called the opposition effect. Its strength depends on the physical properties of the body's surface, and hence it differs from asteroid to asteroid.^[13]

In 1985, the IAU adopted the semi-empirical HGdisplaystyle HG-system, based on two parameters Hdisplaystyle H and Gdisplaystyle G called absolute magnitude and slope, to model the opposition effect for the ephemerides published by the Minor Planet Center.^[20]

m=H+5log10⁡(dBSdBOd02)−2.5log10⁡q(α),displaystyle m=H+5log _10left(frac d_BSd_BOd_0^2right)-2.5log _10q(alpha ),

where

the phase integral is q(α)=(1−G)ϕ1(α)+Gϕ2(α)displaystyle q(alpha )=left(1-Gright)phi _1left(alpha right)+Gphi _2left(alpha right)

and

ϕi(α)=exp⁡(−Ai(tan⁡α2)Bi)displaystyle phi _ileft(alpha right)=exp left(-A_ileft(tan frac alpha 2right)^B_iright) for i=1displaystyle i=1 or 2displaystyle 2, A1=3.332displaystyle A_1=3.332, A2=1.862displaystyle A_2=1.862, B1=0.631displaystyle B_1=0.631 and B2=1.218displaystyle B_2=1.218.^[21]

This relation is valid for phase angles α<120∘displaystyle alpha <120^circ , and works best when α<20∘displaystyle alpha <20^circ .^[22]

The slope parameter Gdisplaystyle G relates to the surge in brightness, typically 6999300000000000000♠0.3 mag, when the object is near opposition. It is known accurately only for a small number of asteroids, hence for most asteroids a value of G=0.15displaystyle G=0.15 is assumed.^[22] In rare cases, Gdisplaystyle G can be negative.^[21][23] An example is 101955 Bennu, with G=−0.08displaystyle G=-0.08.^[24]

In 2012, the HGdisplaystyle HG-system was officially replaced by an improved system with three parameters Hdisplaystyle H, G1displaystyle G_1 and G2displaystyle G_2, which produces more satisfactory results if the opposition effect is very small or restricted to very small phase angles. However, as of 2019, this HG1G2displaystyle HG_1G_2-system has not been adopted by either the Minor Planet Center nor Jet Propulsion Laboratory.^[13][25]

The apparent magnitude of asteroids varies as they rotate, on time scales of seconds to weeks depending on their rotation period, by up to 2 magdisplaystyle 2text mag or more.^[26] In addition, their absolute magnitude can vary with the viewing direction, depending on their axial tilt. In many cases, neither the rotation period nor the axial tilt are known, limiting the predictability. The models presented here do not capture those effects.^[22][13]

Cometary magnitudes

The brightness of comets is given separately as total magnitude (m1displaystyle m_1, the brightness integrated over the entire visible extend of the coma) and nuclear magnitude (m2displaystyle m_2, the brightness of the core region alone).^[27] Both are different scales than the magnitude scale used for planets and asteroids, and can not be used for a size comparison with an asteroid's absolute magnitude H.

The activity of comets varies with their distance from the Sun. Their brightness can be approximated as

m1=M1+2.5⋅K1log10⁡(dBSd0)+5log10⁡(dBOd0)displaystyle m_1=M_1+2.5cdot K_1log _10left(frac d_BSd_0right)+5log _10left(frac d_BOd_0right)

m2=M2+2.5⋅K2log10⁡(dBSd0)+5log10⁡(dBOd0),displaystyle m_2=M_2+2.5cdot K_2log _10left(frac d_BSd_0right)+5log _10left(frac d_BOd_0right),

where m1,2displaystyle m_1,2 are the total and nuclear apparent magnitudes of the comet, respectively, M1,2displaystyle M_1,2 are its "absolute" total and nuclear magnitudes, dBSdisplaystyle d_BS and dBOdisplaystyle d_BO are the body-sun and body-observer distances, d0displaystyle d_0 is the Astronomical Unit, and K1,2displaystyle K_1,2 are the slope parameters characterising the comet's activity. For K=2displaystyle K=2, this reduces to the formula for a purely reflecting body.^[28]

Exampe: The lightcurve of comet C/2011 L4 (PANSTARRS) can be approximated by M1=5.41, K1=3.69.displaystyle M_1=5.41text, K_1=3.69.^[29] On the day of its perihelion passage, 10 March 2013, comet PANSTARRS was 0.302 AUdisplaystyle 0.302text AU from the Sun and 1.109 AUdisplaystyle 1.109text AU from Earth. The total apparent magnitude m1displaystyle m_1 is predicted to have been m1=5.41+2.5⋅3.69⋅log10⁡(0.302)+5log10⁡(1.109)=+0.8displaystyle m_1=5.41+2.5cdot 3.69cdot log _10left(0.302right)+5log _10left(1.109right)=+0.8 at that time. The Minor Planet Center gives a value close to that, m1=+0.5displaystyle m_1=+0.5.^[30]

For some comets that have been observed at heliocentric distances large enough to distinguish between light reflected from the coma, and light from the nucleus itself, an absolute magnitude analogous to that used for asteroids has been calculated, allowing to estimate the sizes of their nuclei.^[31]

Meteors

For a meteor, the standard distance for measurement of magnitudes is at an altitude of 100 km (62 mi) at the observer's zenith.^[32][33]

See also

• Photographic magnitude


• 
  Hertzsprung–Russell diagram – relates absolute magnitude or luminosity versus spectral color or surface temperature.


• 
  Jansky radio astronomer's preferred unit – linear in power/unit area


• 
  Surface brightness – the magnitude for extended objects


• List of most luminous stars

References

External links

• Reference zero-magnitude fluxes


• International Astronomical Union


• Absolute Magnitude of a Star calculator


• The Magnitude system


• About stellar magnitudes


• 
  Obtain the magnitude of any star – SIMBAD
  


• Converting magnitude of minor planets to diameter


• Another table for converting asteroid magnitude to estimated diameter