Xrthnty

漸伸線（involute）(或稱漸開線(evolvent))和漸屈線（evolute）是曲線的微分幾何上互為表裡的概念。若曲線A是曲線B的漸伸線，曲線B是曲線A的漸屈線。

在曲線上選一定點S。有一動點P由S出發沿曲線移動，選在P的切線上的Q，使得曲線長SP 和直線段長PQ 相同。漸伸線就是Q的軌跡。

若曲線B有參數方程r:R→Rndisplaystyle r:mathbb R to mathbb R ^n，其中|r′(s)|=1displaystyle ，曲線A的方程為t↦r(t)−tr′(t)displaystyle tmapsto r(t)-tr^prime (t)。

曲線的漸屈線是該曲線每點的曲率中心的集。

若該曲線有參數方程r:R→Rndisplaystyle r:mathbb R to mathbb R ^n（|r′(s)|=1displaystyle ），則其漸屈線為

s→r(s)+r″(s)|r″(s)|2displaystyle sto r(s)+^2。

每條曲線可有無窮多條漸伸線，但只有一條漸屈線。

參數化曲線

漸開線方程曲線的參數化定義的函數( x(t) , y(t) ) 是:

X[x,y]=x−x′∫atx′2+y′2dtx′2+y′2displaystyle X[x,y]=x-frac x'int _a^tsqrt x'^2+y'^2,dtsqrt x'^2+y'^2

Y[x,y]=y−y′∫atx′2+y′2dtx′2+y′2displaystyle Y[x,y]=y-frac y'int _a^tsqrt x'^2+y'^2,dtsqrt x'^2+y'^2

範例

圓的漸伸線 (反向, by unwinding)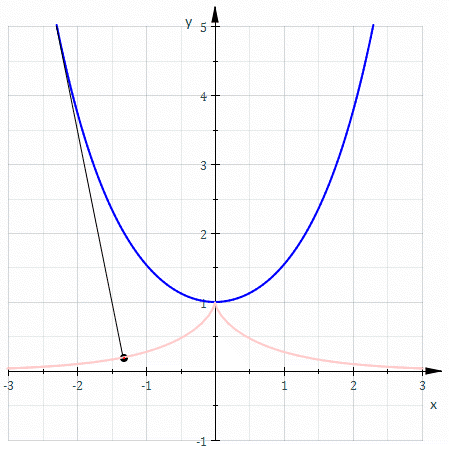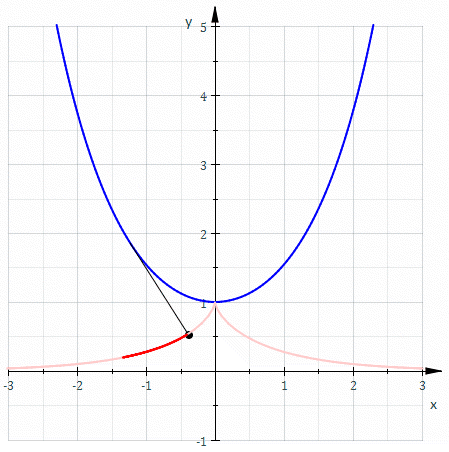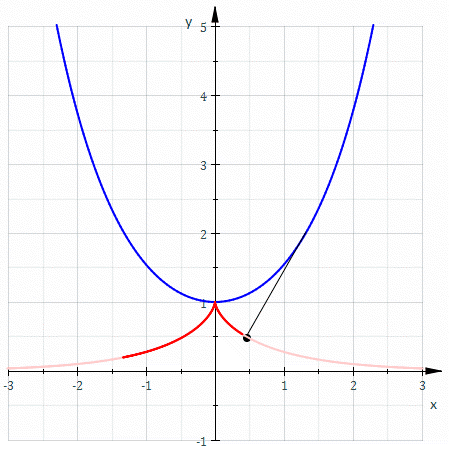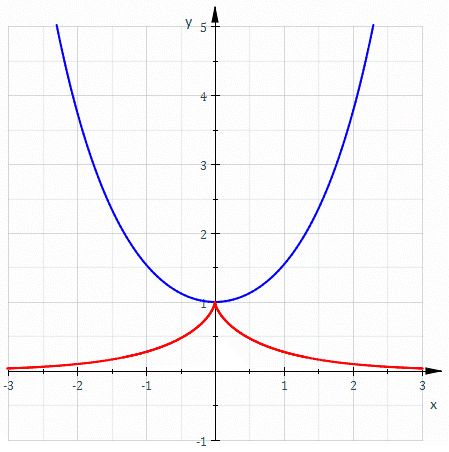

懸鏈線的漸開線是一個 曳物線。

圓的漸伸線

圓的漸伸線會形成一個類似阿基米德螺線的圖形.

• 在笛卡兒坐標系中，一個圓的漸開線的參數方程可以寫成：

x=a(cos⁡ t+tsin⁡ t)displaystyle ,x=aleft(cos t+tsin tright)

y=a(sin⁡ t−tcos⁡ t)displaystyle ,y=aleft(sin t-tcos tright)

其中adisplaystyle ,a是圓的半徑，tdisplaystyle ,t為參數

• 在 極坐標系中， r,θdisplaystyle ,r,theta 一個圓的漸開線的參數方程可以寫成：

r=asec⁡αdisplaystyle ,r=asec alpha

θ=tan⁡α−αdisplaystyle ,theta =tan alpha -alpha

其中 adisplaystyle ,a 是圓的半徑 αdisplaystyle ,alpha 為參數

通常，一個圓的漸開線常被寫成寫成：

r=a1+t2displaystyle ,r=asqrt 1+t^2

θ=arctan⁡cos⁡t+tsin⁡tsin⁡t−tcos⁡tdisplaystyle ,theta =arctan frac cos t+tsin tsin t-tcos t.

歐拉建議使用圓的漸開線作為齒輪的形狀, 這個設計普遍存在於目前使用，稱為漸開線齒輪。

懸鏈線的漸開線

一個懸鏈線的漸開線 會通過此懸鏈線的頂點 ，形成曳物線。 在笛卡兒坐標系中，一個懸鏈線的漸開線的參數方程可以寫成：

x=t−tanh(t)displaystyle x=t-mathrm tanh (t),

y=sech(t)displaystyle y=mathrm sech (t),

其中t 是參數，而sech是雙曲正割函數(1/cosh(x))

衍生

用r(s)=(sinh−1⁡(s),cosh⁡(sinh−1⁡(s)))displaystyle r(s)=(sinh ^-1(s),cosh(sinh ^-1(s))),

我們得到 r′(s)=(1,s)/1+s2displaystyle r^prime (s)=(1,s)/sqrt 1+s^2,

且r(t)−tr′(t)=(sinh−1⁡(t)−t/1+t2,1/1+t2)displaystyle r(t)-tr^prime (t)=(sinh ^-1(t)-t/sqrt 1+t^2,1/sqrt 1+t^2).

替代成 t=1−y2/ydisplaystyle t=sqrt 1-y^2/y

可得到 (sech−1(y)−1−y2,y)displaystyle (rm sech^-1(y)-sqrt 1-y^2,y).

擺線的漸開線

一個 擺線的漸開線是另一個與它 全等的擺線 在笛卡兒坐標系中，一個擺線的漸開線的參數方程可以寫成：

x=r(t−sin⁡(t))displaystyle x=r(t-sin(t)),

y=r(1−cos⁡(t))displaystyle y=r(1-cos(t)),

其中 t 是角度， r 是 半徑

另外參見

• 漸屈線


• 渦旋壓縮機


• 漸開線齒輪

外部連結

• Xah: Special Plane Curves: Involute, Evolute
  


• Mathworld