Xrthnty

三角函数： 正弦、 餘弦、 正切、 餘割（鏈線）、 正割（鏈線）、 餘切（鏈線）

三角函数（英语：Trigonometric functions）是数学中常见的一类关于角度的函数。三角函数将直角三角形的内角和它的两个边的比值相关联，也可以等价地用与单位圆有关的各种线段的长度来定义。三角函数在研究三角形和圆等几何形状的性质时有重要作用，也是研究周期性现象的基础数学工具^[1]。在数学分析中，三角函数也被定义为无穷级数或特定微分方程的解，允许它们的取值扩展到任意实数值，甚至是复数值。

常见的三角函数包括正弦函数（sindisplaystyle sin ）、余弦函数（cosdisplaystyle cos ）和正切函数（tandisplaystyle tan 或者tgdisplaystyle operatorname tg ）^[1]；在航海学、测绘学、工程学等其他学科中，还会用到如余切函数、正割函数、余割函数、正矢函数、半正矢函数等其他的三角函数。不同的三角函数之间的关系可以通过几何直观或者计算得出，称为三角恒等式。

三角函数一般用于计算三角形中未知长度的边和未知的角度，在导航、工程学以及物理学方面都有广泛的用途。另外，以三角函数为模版，可以定义一类相似的函数，叫做双曲函数^[2]。常见的双曲函数也被称为双曲正弦函数、双曲余弦函数等等。

历史

早期对于三角函数的研究可以追溯到古代。例如古埃及数学家在鑑別尼羅河泛濫後的土地邊界、保持金字塔每邊斜度相同，都使用了三角術，只是他們可能還沒有對這種方式定名而已。古希腊三角术的奠基人是公元前2世纪的喜帕恰斯。他按照古巴比伦人的做法，将圆周分为360等份（即圆周的弧度为360度，与现代的弧度制不同）。对于给定的弧度，他给出了对应的弦的长度数值，这个记法和现代的正弦函数是等价的。喜帕恰斯实际上给出了最早的三角函数数值表。然而古希腊的三角学基本是球面三角学。这与古希腊人研究的主体是天文学有关。梅涅劳斯在他的著作《球面学》中使用了正弦来描述球面的梅涅劳斯定理。古希腊三角学与其天文学的应用在埃及的托勒密时代达到了高峰，托勒密在《数学汇编》（Syntaxis Mathematica）中计算了36度角和72度角的正弦值，还给出了计算和角公式和半角公式的方法。托勒密还给出了所有0到180度的所有整数和半整数弧度对应的正弦值^{[3]:133-140[4]:151-152}。

希腊文化传播到古印度后，印度人对三角术进行了进一步的研究。公元5世纪末的数学家阿耶波多提出用弧对应的弦长的一半来对应半弧的正弦，这个做法被後来的古印度数学家使用，和现代的正弦定义一致了^[4]:189。阿耶波多的计算中也使用了余弦和正割。他在计算弦长时使用了不同的单位，重新计算了0到90度中间隔三又四分之三度（3.75°）的三角函数值表^[4]:193。然而古印度的数学与当时的中国一样，停留在计算方面，缺乏系统的定义和演绎的证明。阿拉伯人也采用了古印度人的正弦定义，但他们的三角学是直接继承于古希腊。阿拉伯天文学家引入了正切和余切、正割和余割的概念，并计算了间隔10分（10′）的正弦和正切数值表^[3]:214-215。到了公元14世纪，阿拉伯人将三角计算重新以算术方式代数化（古希腊人采用的是建立在几何上的推导方式）的努力为後来三角学从天文学中独立出来，成为了有更广泛应用的学科奠定了基础。^[3]:225

进入15世纪后，阿拉伯数学文化开始传入欧洲。随着欧洲商业的兴盛，航行、历法测定和地理测绘中出现了对三角学的需求。在翻译阿拉伯数学著作的同时，欧洲数学家开始制作更详细精确的三角函数值表。哥白尼的学生乔治·约阿希姆·瑞提克斯（英语：Goerg Joachim Rheticus）制作了间隔10秒（10″）的正弦表，有9位精确值。瑞提克斯还改变了正弦的定义，原来称弧对应的弦长是正弦，瑞提克斯则将角度对应的弦长称为正弦。16世纪后，数学家开始将古希腊有关球面三角的结果和定理转化为平面三角定理。弗朗索瓦·韦达给出了托勒密的不少结果对应的平面三角形式。他还尝试计算了多倍角正弦的表达方式。^[3]:275-278

18世纪开始，随着解析几何等分析学工具的引进，数学家们开始对三角函数进行分析学上的研究。牛顿在1669年的《分析学》一书中给出了正弦和余弦函数的无穷级数表示。Collins将牛顿的结果告诉了詹姆斯·格列高里，後者进一步给出了正切等三角函数的无穷级数。莱布尼兹在1673年左右也独立得到了这一结果^[5]:162-163。欧拉的《无穷小量分析引论》（Introductio in Analysin Infinitorum，1748年）对建立三角函数的分析处理做了最主要的贡献，他定义三角函数为无穷级数，并表述了欧拉公式，还有使用接近现代的简写sin.、cos.、tang.、cot.、sec.和cosec.。

几何定义

直角三角形中的定义

a, b, h分別為角A的对边、邻边和斜边

在直角三角形中仅有锐角（大小在0到90度之间的角）三角函数的定义^[6]。给定一个锐角θdisplaystyle theta ，可以做出一个直角三角形，使得其中的一个内角是θdisplaystyle theta 。设这个三角形中，θdisplaystyle theta 的对边、邻边和斜边长度分别是a,b,hdisplaystyle a,b,h，那么

θdisplaystyle theta 的正弦是对边与斜边的比值：sin⁡θ=ahdisplaystyle sin theta =frac ah

θdisplaystyle theta 的餘弦是邻边与斜边的比值：cos⁡θ=bhdisplaystyle cos theta =frac bh

θdisplaystyle theta 的正切是对边与邻边的比值：tan⁡θ=abdisplaystyle tan theta =frac ab

θdisplaystyle theta 的余切是邻边与对边的比值：cot⁡θ=badisplaystyle cot theta =frac ba

θdisplaystyle theta 的正割是斜边与邻边的比值：sec⁡θ=hbdisplaystyle sec theta =frac hb

θdisplaystyle theta 的餘割是斜边与对边的比值：csc⁡θ=hadisplaystyle csc theta =frac ha

直角坐标系中的定义

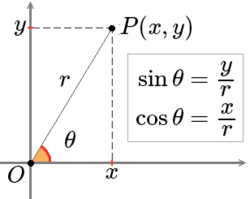
设P( x, y )是平面直角坐标系xOy中的一个点，θ是横轴正向Ox→displaystyle vec Ox逆时针旋转到OP→displaystyle vec OP方向所形成的角，r=x2+y2>0displaystyle r=sqrt x^2+y^2>0是P到原点O的距离，则θ的六个三角函数定义为^[7]：

正弦：	sin⁡θ=yr,displaystyle sin theta =frac yr,	正切：	tan⁡θ=yx,displaystyle tan theta =frac yx,	正割：	sec⁡θ=rx,displaystyle sec theta =frac rx,
餘弦：	cos⁡θ=xr,displaystyle cos theta =frac xr,	餘切：	cot⁡θ=xy,displaystyle cot theta =frac xy,	餘割：	csc⁡θ=ry.displaystyle csc theta =frac ry.

这样可以对0到360度的角度定义三角函数。要注意的是以上的定义都只在定义式有意义的时候成立。比如说当x=0displaystyle x=0
的时候，yxdisplaystyle frac yx和rxdisplaystyle frac rx都没有意义，这说明对于90度角和270度角，正切和正割没有定义。同样地，对于0度角和180度角，余切和余割没有定义。

单位圆定义

三角函数也可以依据直角坐标系xOy中半径为1，圆心为原点O的单位圆来定义^[1]。给定一个角度θ，设A(1, 0)为起始点，如果θ > 0则将OA逆时针转动，如果θ < 0则顺时针移动，直到转过的角度等于θ为止。设最终点A转到的位置为P (x, y)，那么：

用单位圆定义三角函数

这个定义和坐标系的定义类似，但角度θ可以是任何的数值。对于大于360°或小于-360°的角度，可以认为是逆时针（顺时针）旋转了不止一圈。而多转或少转了整数圈不会影响三角函数的取值^[8]。如果按弧度制的方式记录角度，将弧长作为三角函数的输入值（360°等于2π），那么三角函数就是取值为全体实数R，周期为2π的周期函数。比如：

sin⁡θ=sin⁡(θ+2πk),∀θ∈R,k∈Zdisplaystyle sin theta =sin left(theta +2pi kright),quad forall theta in mathbb R ,;;kin mathbb Z

cos⁡θ=cos⁡(θ+2πk),∀θ∈R,k∈Zdisplaystyle cos theta =cos left(theta +2pi kright),quad forall theta in mathbb R ,;;kin mathbb Z

周期函数的最小正周期叫做这个函数的基本周期。正弦、余弦、正割或余割的基本周期是2π弧度或360°；正切或余切的基本周期是π弧度或180°。

基本性质

在直角坐标系平面上f(x) = sin(x)和f(x) = cos(x)函数的图像。

从几何定义中可以推导出很多三角函数的性质。比如说，正弦函数、正切函数、余切函数和余割函数是奇函数，余弦函数和正割函数是偶函数^[9]。正弦和余弦函数的图像形状一样（见右图），可以看作是沿坐标横轴平移得到的两个函数。正弦和余弦函数关于x=π4displaystyle x=frac pi 4轴对称。正切函数和余切函数、正割函数和余割函数也分别如此。

三角恒等式

不同的三角函数之间存在很多对任意的角度取值都成立的等式，被称为三角恒等式。其中最著名的是毕达哥拉斯恒等式，它说明对于任何角，正弦的平方加上余弦的平方总是1^[1]。这可从斜边为1的直角三角形应用勾股定理得出。用符号形式表示，毕达哥拉斯恒等式为：

sin2x+cos2x=1.displaystyle sin ^2!x+cos ^2!x=1.

因此可推導出:

tan2x+1=sec2x.displaystyle tan ^2!x+1=sec ^2!x.

1+cot2x=csc2x.displaystyle 1+cot ^2!x=csc ^2!x.

另一个关键的联系是和差公式，它根据两个角度自身的正弦和余弦而给出它们的和与差的正弦和余弦^[1]。它们可以用几何的方法使用托勒密的论证方法推导出来；还可以用代数方法使用欧拉公式得出。

当两个角相同的时候，和角公式简化为更简单的等式，称为二倍角公式（或倍角公式）。

这些等式还可以用来推导积化和差恒等式^[10]，以前曾用它把两个数的积变换成两个数的和而像对数那样使运算更加快速。（利用制好的三角函数表）

微积分

三角函数的积分和导数可参见导数表、积分表和三角函数积分表。下面是六個基本三角函數的導數和積分的列表。

函数	sin⁡xdisplaystyle , sin x	cos⁡xdisplaystyle , cos x	tan⁡xdisplaystyle , tan x	cot⁡xdisplaystyle , cot x	sec⁡xdisplaystyle , sec x	csc⁡xdisplaystyle , csc x
导函数	cos⁡xdisplaystyle , cos x	−sin⁡xdisplaystyle , -sin x	sec2⁡xdisplaystyle , sec ^2x	−csc2⁡xdisplaystyle , -csc ^2x	sec⁡xtan⁡xdisplaystyle , sec xtan x	−csc⁡xcot⁡xdisplaystyle , -csc xcot x
原函数*	−cos⁡xdisplaystyle , -cos x	sin⁡xdisplaystyle , sin x	−ln⁡|cos⁡x|displaystyle , -ln left	ln⁡|sin⁡x|	ln⁡|sec⁡x+tan⁡x|	ln⁡|csc⁡x−cot⁡x|displaystyle ln left
* 不计常数项

分析学定义

級數定義

正弦函数（蓝色）十分接近于它的7次泰勒级数（粉红色）。

几何学中，三角函数的定义是建立在几何直观上的，只用几何和极限的性质，就可直接获知正弦和餘弦的導數。分析学中，三角函數是解析函數，数学家用泰勒級數给出了不依赖几何直观的代数定义^[11]：

sin⁡x=∑n=0∞(−1)nx2n+1(2n+1)!=x−x33!+x55!−x77!+⋯displaystyle sin x=sum _n=0^infty frac (-1)^nx^2n+1(2n+1)!=x-frac x^33!+frac x^55!-frac x^77!+cdots

cos⁡x=∑n=0∞(−1)nx2n(2n)!=1−x22!+x44!−x66!+⋯displaystyle cos x=sum _n=0^infty frac (-1)^nx^2n(2n)!=1-frac x^22!+frac x^44!-frac x^66!+cdots

可以证明以上的无穷级数对任意实数xdisplaystyle x都是收敛的，所以很好地定义了正弦和余弦函数。

三角函数的级数定义经常被用做三角函数的严格处理和应用的起点（比如，在傅立叶级数中），因为无穷级数的理论可从实数系的基础上发展而来，不需要任何几何方面的考虑。这样，这些函数的可微性和连续性便可以单独从级数定义来确立。

其他三角函数的级数定义：^[12]

tan⁡x=∑n=1∞(−1)n−122n(22n−1)B2nx2n−1(2n)!=x+x33+2x515+17x7315+⋯(|x|<π2)<frac pi 2right)

sec⁡x=∑n=0∞(−1)nEnx2n(2n)!=1+x22+5x424+61x6720+⋯(

^ 清华大学数学科学系《微积分》编写组. 微积分（I）. 清华大学出版社. 2003. ISBN 9787302067856. 

^ ^3.03.13.23.3 莫里斯·克莱因 著，张理京，张锦炎，江泽涵 译. 《古今数学思想》第一册. 上海科学技术出版社. 2002. ISBN 9787532361724. 

^ ^4.04.14.2 Uta C.Merzbach, Carl B. Boyer. A History of Mathematics. John Wiley & Sons, Inc.第3版. 2011. ISBN 978-0-470-52548-7 （英语）. 

^ 莫里斯·克莱因 著，朱学贤，申又枨，叶其孝 译. 《古今数学思想》第二册. 上海科学技术出版社. 2002. ISBN 9787532361731. 

^ 銳角三角函數 (PDF). [2013-12-21]. 

^ 三角函數的定義. Webcai.math.fcu.edu.tw. [2013-12-21]. 

^ 廣義角三角函數 (PDF). [2013-12-21]. 

^ ^9.09.1 谭杰锋, 郑爱武. 高等数学. 清华大学出版社. 2006. 

^ 初三年级. 积化和差公式. Zhongxue.hujiang.com. [2013-12-21]. 

^ Ahlfors, pages 43–44.

^ Abramowitz; Weisstein.

^ Euler (1707-1783) —數學的莎士比亞 (PDF). [2013-12-21]. （原始内容 (PDF)存档于2007-02-08）. 

^ 以微積分方法探討三角函數的性質 (PDF). [2013-12-21]. 

^ Needham, p. ix.

^ Kannappan, Palaniappan. Functional Equations and Inequalities with Applications. Springer. 2009. ISBN 978-0387894911. 

^ 和差角公式. Highscope.ch.ntu.edu.tw. 2011-10-19 [2013-12-21]. 

^ Kantabutra.

^ However, doing that while maintaining precision is nontrivial, and methods like Gal's accurate tables, Cody and Waite reduction, and Payne and Hanek reduction algorithms can be used.

^ R. P. Brent, "Fast Multiple-Precision Evaluation of Elementary Functions", J. ACM '''23''', 242 (1976). Doi.acm.org. [2013-12-21]. doi:10.1145/321941.321944. 

^ 三角函數特殊角的值. Web.ntnu.edu.tw. [2013-12-21]. 

^ 雙曲函數及反三角函數. Stat.nuk.edu.tw. [2013-12-21]. 

^ ^23.023.1 正弦定理與餘弦定理 (PDF). [2013-12-21]. 

^ Eli Maor, Trigonometric Delights, Princeton University Press, 2002.

^ 圓與三角學. Episte.math.ntu.edu.tw. 2004-06-19 [2013-12-21]. 

^ 靳希,杨尔滨,赵玲. 信号处理原理与应用. 清华大学出版社. 2004. ISBN 9787302083573.  |chapter=被忽略 (帮助)

^ 邓翔宇. 信号与系统. 清华大学出版社. 2006. ISBN 9787810827058.  |chapter=被忽略 (帮助)

参考文献

• Abramowitz, Milton、Irene A. Stegun，Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables，Dover，New York（1964年），ISBN 978-0-486-61272-0。


• Boyer, Carl B.，A History of Mathematics，John Wiley & Sons, Inc.，第二版（1991年），ISBN 978-0-471-54397-8。


• Joseph, George G.，The Crest of the Peacock: Non-European Roots of Mathematics，第二版，Penguin Books，London，（2000年），ISBN 978-0-691-00659-8。


• Kantabutra, Vitit，On hardware for computing exponential and trigonometric functions，IEEE Trans. Computers 45 (3), 328-339（1996年）。


• Maor, Eli，Trigonometric Delights，Princeton Univ. Press.（1998年），重印版（2005年2月25日）：ISBN 978-0-691-09541-7。


• Needham, Tristan，Preface，Visual Complex Analysis，Oxford University Press，（1999年），ISBN 978-0-19-853446-4。


• O'Connor, J.J.、E.F. Robertson，Trigonometric functions，MacTutor History of Mathematics Archive，（1996年）。


• O'Connor, J.J.、E.F. Robertson，Madhava of Sangamagramma，MacTutor History of Mathematics Archive，（2000年）。


• Pearce, Ian G.，Madhava of Sangamagramma，MacTutor History of Mathematics Archive，（2002年）。


• Weisstein, Eric W.，Tangent，MathWorld，2006年1月21日访问。


• Lars Ahlfors, Complex Analysis: an introduction to the theory of analytic functions of one complex variable, second edition, McGraw-Hill Book Company, New York, 1966.

外部链接

• Engineers Edge的三角函數列表


• 
  nanoSouffle線上繪圖─可繪畫各種函數。可在各瀏覽器使用，JavaScript只用於實時更新，並非必須


• 
  正弦和餘弦函數─以REXX來表示


• 
  以角度和弧度表示的角所對應的函數值^{[失效連結]}


• 單位圓教學Flash動畫


• 常用三角函數表（文字版）

查 论 编 三角函數 基本函數 正弦 · 餘弦 · 正切 · 餘切 · 正割 · 餘割 反函數 反正弦 · 反餘弦 · 反正切 · 反餘切 · 反正割‎ · 反餘割 其他函數 正矢 · 餘矢 · cis函數 · 餘cis函數 · 半正矢 · 半餘矢 · 外正割 · 外餘割 · atan2 · 古德曼函數 定理 正弦定理 · 餘弦定理 · 正切定理 · 餘切定理 · 正割定理 · 勾股定理 其他 三角函數恆等式 · 三角函數精確值 · 三角函数积分表 · 三角函数表 · 雙曲三角函數 · 雙曲三角函數恆等式

规范控制 NDL: 00570156