几何中心

几何中心

Clash Royale CLAN TAG#URR8PPP

三角形的中心

n 维空间中一个对象X的几何中心或形心是将X分成矩相等的两部分的所有超平面的交点。非正式地说，它是X中所有点的平均。如果一個物件質量分佈平均，形心便是重心。

如果一个对象具有一致的密度，或者其形状和密度具有某种对称性足以确定几何中心，那么它的几何中心和质量中心重合，该条件是充分但不是必要的。

有限个点总存在几何中心，可以通过计算这些点的每个坐标分量的算术平均值得到。这个中心是空间中一点到这有限个点距离的平方和的唯一最小值点。点集的几何中心在仿射变换下保持不变。

目录

1 性質

2 三角形的中心
- 2.1 三條中線共點證明
- 2.2 中心分中线为2:1的证明
- 2.3 性質

3 四面体的中心

4 多边形的中心

5 有限点集的中心

6 面积中心

7 积分公式

8 圆锥和棱锥的中心

9 对称中心

10 地理中心

11 参见

12 参考文献

13 外部链接

性質

一个凸对象的几何中心总在其内部。一个非凸对象的几何中心可能在外部，比如一个环或碗的几何中心不在内部。

三角形的中心

Triangle centroid 1.svg

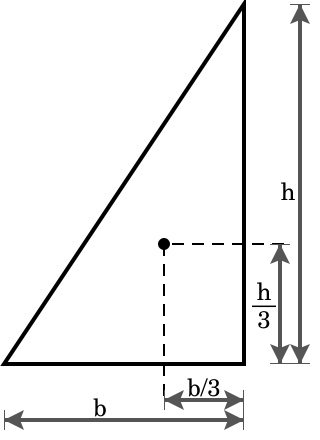Triangle centroid 2.svg

形心是三角形的幾何中心，通常也称为重心，三角形的三條中线（頂點和對邊的中點的連線）交點，此點即為重心^[1]。

三條中線共點證明

三條中線共點證明

用西瓦定理逆定理可以直接證出：

fracBEEC cdot fracCFFA cdot fracADDB=frac11 cdot frac11 cdot frac11=1

因此三線共點。^[2]

中心分每条中线比为2:1，这就是说距一边的距离是该边相对顶点距该边的1/3。如右图所示：

如果三角形是由均匀材料做成的薄片，那么几何中心也就是质量中心。它的笛卡尔坐标是三个顶点的坐标算术平均值。也就是说，如果三顶点位于 $(x_a, y_a)$ ， $(x_b, y_b)$ ，和 $(x_c, y_c)$ ，那么几何中心位于：

Big(

三角形的中心一般用字母G表示。在任何一个三角形中，外心O、中心M、九点圆圆心F和垂心H四点共线，且 $overlineOG:overlineOF:overlineOH = 1: 2: 3$ 。这个定理最早由欧拉证明，故称为欧拉定理，这条线称为欧拉线。类似的有，内心I、中心G和奈格尔点N三点共线，且 $overlineIG: overlineIN = 1: 3$ 。

三角形中心的等角共轭点称为类似重心。

中心分中线为2:1的证明

设三角形ABC的中线AD，BE和CF交于三角形的中心G，延长AD至点O使得

AG = GO. ,

那么三角形AGE和AOC 相似（公共角A，AO = 2 AG，AC = 2 AE），所以OC平行于GE。但是GE是BG的延长，所以OC平行于BG。同样的，OB平行于CG。

从而图形GBOC是一个平行四边形。因为平行四边形对角线互相平分，对角线GO和BC的交点使得GD = DO，这样

GO = GD + DO = 2GD. ,

所以， $AG = GO = 2GD,$ ，或 $AG:GD = 2: 1,$ ，这对任何中线都成立。

性質

三角形的重心與三頂點連線，所形成的三個三角形面積相等。

頂點到重心的距離是中線的 $tfrac23$ 。

重心、外心、垂心、九點圓圓心四點共線。^[3]

重心、內心、奈格爾點、類似重心四點共線。

三角形的重心同時也是中點三角形的重心。

在直角座標系中，若頂點的座標分別為 $(x_1,y_1)$ 、 $(x_2,y_2)$ 、 $(x_3,y_3)$ ，則中點的座標為：

left(fracx_1+x_2+x_33,fracy_1+y_2+y_33right)

三線坐標中、重心的座標為：

bc : ca : ab = frac1a : frac1b : frac1c = csc A : csc B : csc C

四面体的中心

类似三角形的中心的结论对四面体也成立，四面体的几何中心是所有顶点和相对平面中心的连线的交点。这些线段被中心分成3:1。这个结论能自然推广到任何 $n$ -维单形。如果单形的顶点集是 $v_0,...,v_n$ ，将这些顶点看成向量，几何中心位于：

frac1n+1sum_i=0^n v_i ; .

多边形的中心

一个由N个顶点（x_i , y_i）确定的不自交闭多边形的中心能如下计算：
^[4]

记号（ x_N , y_N）与顶点（ x₀ , y₀）相同。多边形的面积为：

A = frac12sum_i=0^N-1(x_i y_i+1 - x_i+1 y_i)

多边形的中心由下式给出：

C_x = frac16Asum_i=0^N-1(x_i+x_i+1)(x_i y_i+1 - x_i+1 y_i)

C_y = frac16Asum_i=0^N-1(y_i+y_i+1)(x_i y_i+1 - x_i+1 y_i)

有限点集的中心

给定有限点集 $x_1,x_2,ldots,x_k$ 属于 $mathbb R ^n$ ，它们的中心定义 $C$ 为

C = fracx_1+x_2+cdots+x_kk

。

面积中心

面积中心和质量中心非常类似，面积中心只取决于图形的几何形状。如果物体是均匀的，质量中心将位于面积中心。
^[5]

对于两部分组成的图形，将有如下等式：

overliney = dfracoverliney_1A_1 + overliney_2A_2A_1 + A_2

$overliney$ 是特定部分的面积中心到所选参考系的距离。 $A$ 是特定部分的面积。

当一个复杂几何图形可以分成一些已知的简单几何图形时，先计算各部分的面积中心，然后通过下面一般的公式计算整个图形的面积中心：

overlinex = fracsum overlinex_iA_isum A_i

overliney = fracsum overliney_iA_isum A_i

这里从y-轴到中心的距离是 $overline x$ ，从x-轴到中心的距离是 $overliney$ ，中心的坐标是 $(overlinex , overliney)$ 。

积分公式

一个平面图形的中心的横坐标（x轴）由积分

C_x = fracint x f(x) ; dxint f(x) ; dx

给出。

这里f（x）是对象位于在横坐标x点y轴上的长度，是在x图形的测度。这个公式能由区域关于y-轴的第一矩得出。

这个过程等价于取加权平均。假设y-轴表示频率，x-轴表示欲求平均值的变量，那么沿着x-轴的中心即 $barx$ 。从而中心可以想象成表示特定形状的许多无限小元的加权平均。

对任意维数n，由相同的公式得出 $R^n$ 中一个对象的中心第一个坐标，假设f (x)是对象在坐标x的截面（也就是说，对象中第一个坐标为x的所有点的集合）的（n-1）-维测度。

注意到分母恰是对象的n- 维测度。特别的，在f为正规时，即分母为1，中心也称为f的平均。

当对象的测度为0或者积分发散，这个公式无效。

圆锥和棱锥的中心

圆锥或棱锥的中心位于连接顶点和底的中心的线段上，分比为3:1。

对称中心

如果中心确定了，那么中心是所有它对称群的不动点。从而对称能全部或部分确定中心，取决于对称的种类。另外可以知道，如果一个对象具有传递对称性，那么它的中心是不确定的或不在内部，因为一个传递变换群没有不动点。

地理中心

地理学中，地球表面一个区域的几何中心也称为地理中心。

参见

重心列表

帕普斯中心定理

K-平均算法

中點

外心

內心

垂心

奈格爾點

類似中線

歐拉線

西瓦定理

参考文献

^ 幾何原本ISBN 957-603-016-1

^ 幾何明珠ISBN 957-603-197-4

^ 歐拉線

^ Calculating the area and centroid of a polygon 互联网档案馆的存檔，存档日期2008-10-16.

^ Area Centroid

外部链接

Encyclopedia of Triangle Centers by Clark Kimberling. The centroid is indexed as X (2).

Triangle centers by Antonio Gutierrez from Geometry Step by Step from the Land of the Incas.

Characteristic Property of Centroid at cut-the-knot

Barycentric Coordinates at cut-the-knot

Online Tool to Compute Center of Mass bounded by f (x) and g (x)

Interactive animations showing Centroid of a triangle and Centroid construction with compass and straightedge