Tensile structure

 Clash Royale CLAN TAG#URR8PPP
Clash Royale CLAN TAG#URR8PPP
This article includes a list of references, but its sources remain unclear because it has insufficient inline citations. (September 2011) (Learn how and when to remove this template message) |

The world's first tensile steel Shell by Vladimir Shukhov (during construction), Nizhny Novgorod, 1895

The Sidney Myer Music Bowl in Kings Domain, Melbourne
A tensile structure is a construction of elements carrying only tension and no compression or bending. The term tensile should not be confused with tensegrity, which is a structural form with both tension and compression elements.
Tensile structures are the most common type of thin-shell structures.
Most tensile structures are supported by some form of compression or bending elements, such as masts (as in The O2, formerly the Millennium Dome), compression rings or beams.
A tensile membrane structure is most often used as a roof, as they can economically and attractively span large distances. Tensile membrane structures may also be used as complete buildings, with a few common applications being sports facilities, warehousing and storage buildings, and exhibition venues.[1]
Contents
1 History
2 Types of structure with significant tension members
2.1 Linear structures
2.2 Three-dimensional structures
2.3 Surface-stressed structures
3 Cable and membrane structures
3.1 Membrane materials
3.2 Cables
3.3 Structural forms
3.4 Form-finding
3.5 Pretension
3.6 Alternative form-finding approach
4 Simple mathematics of cables
4.1 Transversely and uniformly loaded cable
4.2 Cable with central point load
5 Tensioned cable oscillations
6 Notable structures
7 Gallery of well-known tensile structures
8 Classification numbers
9 See also
10 References
11 Further reading
History

The Olympiastadion in Munich makes extensive use of tensile roofing structures.
This form of construction has only become more rigorously analyzed and widespread in large structures in the latter part of the twentieth century. Tensile structures have long been used in tents, where the guy ropes and tent poles provide pre-tension to the fabric and allow it to withstand loads.
Russian engineer Vladimir Shukhov was one of the first to develop practical calculations of stresses and deformations of tensile structures, shells and membranes. Shukhov designed eight tensile structures and thin-shell structures exhibition pavilions for the Nizhny Novgorod Fair of 1896, covering the area of 27,000 square meters. A more recent large-scale use of a membrane-covered tensile structure is the Sidney Myer Music Bowl, constructed in 1958.
Antonio Gaudi used the concept in reverse to create a compression-only structure for the Colonia Guell Church. He created a hanging tensile model of the church to calculate the compression forces and to experimentally determine the column and vault geometries.
The concept was later championed by German architect and engineer Frei Otto, whose first use of the idea was in the construction of the West German pavilion at Expo 67 in Montreal. Otto next used the idea for the roof of the Olympic Stadium for the 1972 Summer Olympics in Munich.
Since the 1960s, tensile structures have been promoted by designers and engineers such as Ove Arup, Buro Happold, Walter Bird of Birdair, Inc., Frei Otto, Mahmoud Bodo Rasch, Eero Saarinen, Horst Berger, Matthew Nowicki, Jörg Schlaich, the duo of Nicholas Goldsmith & Todd Dalland at FTL Design & Engineering Studio and David Geiger.
Steady technological progress has increased the popularity of fabric-roofed structures. The low weight of the materials makes construction easier and cheaper than standard designs, especially when vast open spaces have to be covered.
Types of structure with significant tension members
Linear structures
- Suspension bridges
- Draped cables
Cable-stayed beams or trusses- Cable trusses
- Straight tensioned cables
Three-dimensional structures
Bicycle wheel (can be used as a roof in a horizontal orientation)- 3D cable trusses
Tensegrity structures
Surface-stressed structures
- Prestressed membranes
- Pneumatically stressed membranes
- Gridshell
- Fabric structure
Cable and membrane structures

The world's first steel membrane roof and lattice steel shell in the Shukhov Rotunda, Russia, 1895
Membrane materials
Common materials for doubly curved fabric structures are PTFE-coated fiberglass and PVC-coated polyester. These are woven materials with different strengths in different directions. The warp fibers (those fibers which are originally straight—equivalent to the starting fibers on a loom) can carry greater load than the weft or fill fibers, which are woven between the warp fibers.
Other structures make use of ETFE film, either as single layer or in cushion form (which can be inflated, to provide good insulation properties or for aesthetic effect—as on the Allianz Arena in Munich). ETFE cushions can also be etched with patterns in order to let different levels of light through when inflated to different levels.
In daylight, fabric membrane translucency offers soft diffused naturally lit spaces, while at night, artificial lighting can be used to create an ambient exterior luminescence. They are most often supported by a structural frame as they cannot derive their strength from double curvature.
Cables

Simple suspended bridge working entirely in tension
Cables can be of mild steel, high strength steel (drawn carbon steel), stainless steel, polyester or aramid fibres. Structural cables are made of a series of small strands twisted or bound together to form a much larger cable. Steel cables are either spiral strand, where circular rods are twisted together and "glued" using a polymer, or locked coil strand, where individual interlocking steel strands form the cable (often with a spiral strand core).
Spiral strand is slightly weaker than locked coil strand. Steel spiral strand cables have a Young's modulus, E of 150±10 kN/mm² (or 150±10 GPa) and come in sizes from 3 to 90 mm diameter.[citation needed] Spiral strand suffers from construction stretch, where the strands compact when the cable is loaded. This is normally removed by pre-stretching the cable and cycling the load up and down to 45% of the ultimate tensile load.
Locked coil strand typically has a Young's Modulus of 160±10 kN/mm² and comes in sizes from 20 mm to 160 mm diameter.
The properties of the individuals strands of different materials are shown in the table below, where UTS is ultimate tensile strength, or the breaking load:
E (GPa) | UTS (MPa) | Strain at 50% of UTS | |
|---|---|---|---|
| Solid steel bar | 210 | 400–800 | 0.24% |
| Steel strand | 170 | 1550–1770 | 1% |
| Wire rope | 112 | 1550–1770 | 1.5% |
| Polyester fibre | 7.5 | 910 | 6% |
| Aramid fibre | 112 | 2800 | 2.5% |
Structural forms
Air-supported structures are a form of tensile structures where the fabric envelope is supported by pressurised air only.
The majority of fabric structures derive their strength from their doubly curved shape. By forcing the fabric to take on double-curvature the fabric gains sufficient stiffness to withstand the loads it is subjected to (for example wind and snow loads). In order to induce an adequately doubly curved form it is most often necessary to pretension or prestress the fabric or its supporting structure.
Form-finding
The behaviour of structures which depend upon prestress to attain their strength is non-linear, so anything other than a very simple cable has, until the 1990s, been very difficult to design. The most common way to design doubly curved fabric structures was to construct scale models of the final buildings in order to understand their behaviour and to conduct form-finding exercises. Such scale models often employed stocking material or tights, or soap film, as they behave in a very similar way to structural fabrics (they cannot carry shear).
Soap films have uniform stress in every direction and require a closed boundary to form. They naturally form a minimal surface—the form with minimal area and embodying minimal energy. They are however very difficult to measure. For a large film, its weight can seriously affect its form.
For a membrane with curvature in two directions, the basic equation of equilibrium is:
w=t1R1+t2R2displaystyle w=frac t_1R_1+frac t_2R_2
where:
R1 and R2 are the principal radii of curvature for soap films or the directions of the warp and weft for fabrics
t1 and t2 are the tensions in the relevant directions
w is the load per square metre
Lines of principal curvature have no twist and intersect other lines of principal curvature at right angles.
A geodesic or geodetic line is usually the shortest line between two points on the surface. These lines are typically used when defining the cutting pattern seam-lines. This is due to their relative straightness after the planar cloths have been generated, resulting in lower cloth wastage and closer alignment with the fabric weave.
In a pre-stressed but unloaded surface w = 0, so t1R1=−t2R2displaystyle frac t_1R_1=-frac t_2R_2
In a soap film surface tensions are uniform in both directions, so R1 = −R2.
It is now possible to use powerful non-linear numerical analysis programs (or finite element analysis) to formfind and design fabric and cable structures. The programs must allow for large deflections.
The final shape, or form, of a fabric structure depends upon:
- shape, or pattern, of the fabric
- the geometry of the supporting structure (such as masts, cables, ringbeams etc.)
- the pretension applied to the fabric or its supporting structure

Hyperbolic paraboloid
It is important that the final form will not allow ponding of water, as this can deform the membrane and lead to local failure or progressive failure of the entire structure.
Snow loading can be a serious problem for membrane structure, as the snow often will not flow off the structure as water will. For example, this has in the past caused the (temporary) collapse of the Hubert H. Humphrey Metrodome, an air-inflated structure in Minneapolis, Minnesota. Some structures prone to ponding use heating to melt snow which settles on them.
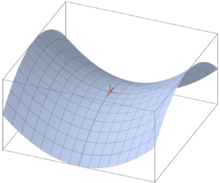
Saddle Shape
There are many different doubly curved forms, many of which have special mathematical properties. The most basic doubly curved from is the saddle shape, which can be a hyperbolic paraboloid (not all saddle shapes are hyperbolic paraboloids). This is a double ruled surface and is often used in both in lightweight shell structures (see hyperboloid structures). True ruled surfaces are rarely found in tensile structures. Other forms are anticlastic saddles, various radial, conical tent forms and any combination of them.
Pretension
Pretension is tension artificially induced in the structural elements in addition to any self-weight or imposed loads they may carry. It is used to ensure that the normally very flexible structural elements remain stiff under all possible loads.
A day to day example of pretension is a shelving unit supported by wires running from floor to ceiling. The wires hold the shelves in place because they are tensioned – if the wires were slack the system would not work.
Pretension can be applied to a membrane by stretching it from its edges or by pretensioning cables which support it and hence changing its shape. The level of pretension applied determines the shape of a membrane structure.
Alternative form-finding approach
The alternative approximated approach to the form-finding problem solution is based on the total energy balance of a grid-nodal system. Due to its physical meaning this approach is called the Stretched Grid Method (SGM).
Simple mathematics of cables
Transversely and uniformly loaded cable
A uniformly loaded cable spanning between two supports forms a curve intermediate between a catenary curve and a parabola. The simplifying assumption can be made that it approximates a circular arc (of radius R).

By equilibrium:
The horizontal and vertical reactions :
- H=wS28ddisplaystyle H=frac wS^28d
- V=wS2{displaystyle V=frac wS2
By geometry:
The length of the cable:
- L=2RarcsinS2Rdisplaystyle L=2Rarcsin frac S2R
The tension in the cable:
- T=H2+V2displaystyle T=sqrt H^2+V^2
By substitution:
- T=(wS28d)2+(wS2)2displaystyle T=sqrt left(frac wS^28dright)^2+left(frac wS2right)^2
The tension is also equal to:
- T=wRdisplaystyle T=wR
The extension of the cable upon being loaded is (from Hooke's Law, where the axial stiffness, k, is equal to k=EALdisplaystyle k=frac EAL
- e=TLEAdisplaystyle e=frac TLEA
where E is the Young's modulus of the cable and A is its cross-sectional area.
If an initial pretension, T0displaystyle T_0
- e=L−L0=L0(T−T0)EAdisplaystyle e=L-L_0=frac L_0(T-T_0)EA
Combining the above equations gives:
- L0(T−T0)EA+L0=2Tarcsin(wS2T)wdisplaystyle frac L_0(T-T_0)EA+L_0=frac 2Tarcsin(frac wS2T)w
By plotting the left hand side of this equation against T, and plotting the right hand side on the same axes, also against T, the intersection will give the actual equilibrium tension in the cable for a given loading w and a given pretension T0displaystyle T_0
Cable with central point load
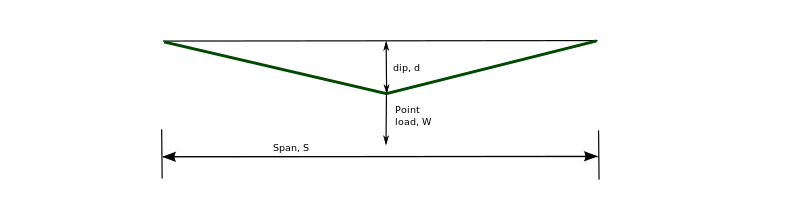
A similar solution to that above can be derived where:
By equilibrium:
- W=4TdLdisplaystyle W=frac 4TdL
- d=WL4Tdisplaystyle d=frac WL4T
By geometry:
- L=S2+4d2=S2+4(WL4T)2displaystyle L=sqrt S^2+4d^2=sqrt S^2+4left(frac WL4Tright)^2
This gives the following relationship:
- L0+L0(T−T0)EA=S2+4(W(L0+L0(T−T0)EA)4T)2displaystyle L_0+frac L_0(T-T_0)EA=sqrt S^2+4left(frac W(L_0+frac L_0(T-T_0)EA)4Tright)^2
As before, plotting the left hand side and right hand side of the equation against the tension, T, will give the equilibrium tension for a given pretension, T0displaystyle T_0
Tensioned cable oscillations
The fundamental natural frequency, f1 of tensioned cables is given by:
- f1=(Tm)2Ldisplaystyle f_1=frac sqrt (frac Tm)2L
where: T = tension in newtons, m = mass in kilograms and L = span length.
Notable structures
@media all and (max-width:720px).mw-parser-output .mobile-float-resetfloat:none!important;width:100%!important.mw-parser-output .stack-containerbox-sizing:border-box.mw-parser-output .stack-clear-leftfloat:left;clear:left.mw-parser-output .stack-clear-rightfloat:right;clear:right.mw-parser-output .stack-leftfloat:left.mw-parser-output .stack-rightfloat:right.mw-parser-output .stack-objectmargin:1px;overflow:hidden
Shukhov Rotunda, Russia, 1896
Canada Place, Vancouver, British Columbia for Expo '86
Yoyogi National Gymnasium by Kenzo Tange, Yoyogi Park, Tokyo, Japan
Ingalls Rink, Yale University by Eero Saarinen
Khan Shatyry Entertainment Center, Astana, Kazakhstan
Tropicana Field, St. Petersburg, Florida
Olympiapark, Munich by Frei Otto
Sidney Myer Music Bowl, Melbourne
The O2 (formerly the Millennium Dome), London by Buro Happold and Richard Rogers Partnership
Denver International Airport, Denver
Dorton Arena, Raleigh
Georgia Dome, Atlanta, Georgia by Heery and Weidlinger Associates (demolished in 2017)
Grantley Adams International Airport, Christ Church, Barbados
Pengrowth Saddledome, Calgary by Graham McCourt Architects and Jan Bobrowski and Partners
Scandinavium, Gothenburg, Sweden- Hong Kong Museum of Coastal Defence
- Modernization of the Central Railway Station, Sofia, Bulgaria
Redbird Arena, Illinois State University, Normal, Illinois- Retractable Umbrellas, Al-Masjid an-Nabawi, Medina, Saudi Arabia
Killesberg Tower, Stuttgart
Gallery of well-known tensile structures

The roof tensile structures by Frei Otto of the Olympiapark, Munich

The Millennium Dome (now The O2), London, by Buro Happold and Richard Rogers

Denver International Airport terminal

The THTR-300 cable-net dry cooling tower, hyperboloid structure by Schlaich Bergermann & Partner

Killesberg Tower, Stuttgart, by Schlaich Bergermann Partner

Georgia Dome in Atlanta

Large Retractable Umbrellas in front of the Prophet’s Holy Mosque in Medina by SL Rasch GmbH Special and Lightweight Structures

Daytime computer render of Khan Shatyr Entertainment Center, the highest tensile structure in the world
Classification numbers
Construction Specifications Institute (CSI) Division 13 MasterFormat 2004 Edition:
- 13 31 23 – Tensioned Fabric Structures
- 13 31 00 – Fabric Structures
- 13 31 33 – Framed Fabric Structures
CSI MasterFormat 1995 Edition:
- 13120 – Cable-Supported Structures
- 13120 – Fabric Structures
See also
- Buckminster Fuller
- Gaussian curvature
- Geodesic dome
- Geodesics
- Hyperboloid structure
- Kārlis Johansons
- Kenneth Snelson
- Suspension bridge
- Tensairity
- Tensegrity
- Wire rope
References
^ plc, Collinson. "Tensile Fabric Structures: The Ultimate Guide (New For 2018)". info.collinson.co.uk. Retrieved 2018-07-02..mw-parser-output cite.citationfont-style:inherit.mw-parser-output .citation qquotes:"""""""'""'".mw-parser-output .citation .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .citation .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-ws-icon abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center.mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-maintdisplay:none;color:#33aa33;margin-left:0.3em.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em
Further reading
- "The Nijni-Novgorod exhibition: Water tower, room under construction, springing of 91 feet span", "The Engineer", № 19.3.1897, P.292-294, London, 1897.
Horst Berger, Light structures, structures of light: The art and engineering of tensile architecture (Birkhäuser Verlag, 1996)
ISBN 3-7643-5352-X- Alan Holgate, The Art of Structural Engineering: The Work of Jorg Schlaich and his Team (Books Britain, 1996)
ISBN 3-930698-67-6
Elizabeth Cooper English: "Arkhitektura i mnimosti": The origins of Soviet avant-garde rationalist architecture in the Russian mystical-philosophical and mathematical intellectual tradition", a dissertation in architecture, 264 p., University of Pennsylvania, 2000.- "Vladimir G. Suchov 1853–1939. Die Kunst der sparsamen Konstruktion.", Rainer Graefe, Jos Tomlow und andere, 192 S., Deutsche Verlags-Anstalt, Stuttgart, 1990,
ISBN 3-421-02984-9.
| Wikimedia Commons has media related to Tensile structures. |
Conrad Roland: Frei Otto – Spannweiten. Ideen und Versuche zum Leichtbau. Ein Werkstattbericht von Conrad Roland. Ullstein, Berlin, Frankfurt/Main und Wien 1965.- Frei Otto, Bodo Rasch: Finding Form - Towards an Architecture of the Minimal, Edition Axel Menges, 1996,
ISBN 3930698668 - Nerdinger, Winfried: Frei Otto. Das Gesamtwerk: Leicht Bauen Natürlich Gestalten, 2005,
ISBN 3-7643-7233-8























